Newton力学・特殊相対論・一般相対論の違いが分かりやすいように表にしてみた

大学に入ってから何度となく相対性理論の勉強に取り組んでは、その難易度に跳ね返されをかれこれ数回繰り返しています。

ちょっとずつでもトライするたびにちょっとずつでも進んでいかなければなと思い、Newton力学、特殊相対論、一般相対論でそれぞれ違くなる部分をわかりやすいように表形式でまとめてみました。

相対性理論に関して学べるおすすめ本!【一般向けの啓蒙書から専門書まで】

「時間が遅れる」「空間が曲がる」など、非常に難解だけれども現象としておもしろい相対性理論。これらに関して学べる本を選んでみました。

啓蒙書から、最終的には専門書までを難易度順に並べています（数学書は別）。後半、僕自身読めていないのもありますが、友人などの意見も交えてのものになります。

相対論と原発・原爆の仕組み「HIROSHIMA・NAGASAKI・FUKUSHIMA」とアインシュタインが望んだ世界

対象:制限なし

数式:なし

 

元記事①:子どもに「相対性理論って何？」と聞かれたときのために概要を分かりやすく簡単に解説してみた 

元記事②:中学校で習う数学の範囲でアインシュタインの相対性理論を分かりやすく解説する

 

この記事は元記事の補完的な役割を果たしていますが、元記事を読まなくてもわかるようにしてあります。

 

はじめに

日本は原発事故を起こし、原爆を落とされ、つくづく原子力と縁のある国だと思います。そんな原子力ですが、もともとはアインシュタインの相対性理論からうまれたものだというのは、思った以上に広まっていないのではと思います。また誤った情報が広がっています。今回は、原子力の仕組みと、それと相対性理論との関係を説明していきたいと思います。

 

アインシュタインの式

元記事を読まれていない方へ

元記事から来た方はスキップしてもらって構わないのですが、この記事から読まれている方のためにアインシュタインの式というのを簡単に説明しておきます。

アインシュタインの式とは

のことです。ここで、それぞれのパラメーターは

:エネルギー

:質量*1

:光速(光の速さ)

のことを表しています。

おそらくほとんどの人が目にしたことがあるように、この式は物理学の中で、最も有名な式だと思います。すごくあっさりとこの式の意味を言うと

エネルギーと質量は比例する

というものです。

つまり重いものはそれだけでエネルギーが大きく、軽いものはエネルギーが小さいということです。

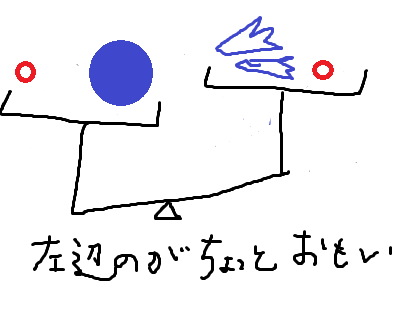
ここで注意してほしいのは、体重が重い人が軽い人の方よりも力があるということではなく、「重さを全てエネルギーに変換すると」重い人の方がエネルギーが大きくなるということです。

 

これ「エネルギーと質量は比例する」ということの何が凄いのかが分かりづらいのでもう少し説明すると、「エネルギー」という意味を根底から覆すものだったから凄いのです。

今まで「エネルギー」とは、何らかの力*2が働いていたり、ものが動いていたり・熱があったり、電気が流れていたり、僕らの直観で「あっ、何かエネルギーが働いてそう」と思えるものだけがエネルギーと呼ばれていました*3。

しかしは、「何もしていなくても質量さえあれば、それはエネルギーになる」ということになります。そう、例えそれが熱がなくても、止まっていても。

あまり使われない言葉ですが、物理では「静止エネルギー」という言葉があります。

静止エネルギーですよ。常識的に考えて何もしてないのにエネルギーなんてあるわけないやん…って思いますよね。こういった非常識的なことを表しているのがであるのです。

 

エネルギーも質量も、元は別なものだと考えられていました。難しい言葉で「エネルギー保存則」と「質量保存の法則」という言葉があります。それぞれ、エネルギーと質量が保存されるということです。何もないところからエネルギーは生まれないし、何もないところから質量のあるものは生まれない。そう考えられていました。

 

しかしによれば、エネルギーが減って質量がうまれたり、質量が減ってエネルギーがうまれたりする。エネルギーと質量は、それぞれ保存されるものではなく、「エネルギー＋質量」と合計で保存されるものだったのです。

 

余談ですが、物理のこういった概念的に分かりづらく、非日常的なことというのは、基本的に数式によって予言されることが多いです。*4

こういったことを見ると数学というものの可能性を感じますよね。

 

話をもどして、言いたいことは、「エネルギーと質量が、変換できるもの！」ということなのです。物理では「エネルギーと質量の等価性」という言葉で言われます。

そして、ただ変換されるだけでなく、エネルギーと質量が比例することまでつきつめました。これがです。

 

化学反応と、質量保存というウソ

これが原子力発電とどのような関係があるのかを見ていきます。

原子力発電の原理はこちらのサイト(原子力発電 － 発電のしくみ ｜ 電気事業連合会)が非常に分かりやすいです。ここでは簡単に要点のみ説明します。

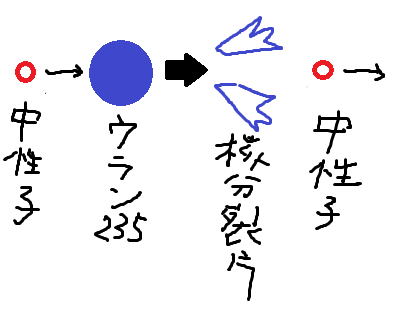
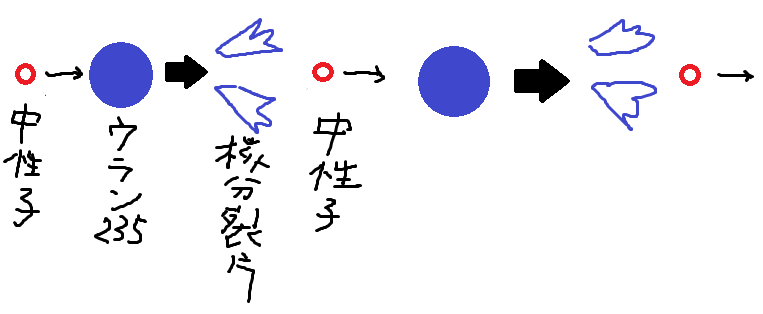
ウラン核分裂反応

ウランという物質を例にとります。

ウランという原子は、「ウラン238」と「ウラン235」とあります。「ウラン238」は基本的に安全な原子なのですが、ウラン235の方が危険なものになります。何が危険なのかというのを一つ一つ説明します。

 

ウラン235に「中性子」という粒子を衝突させると、核分裂を起こして2つ以上の「核分裂片」と「中性子」を放出します。

このとき、核分裂反応によって、再び「中性子」を出すことに注目してください*5。この出された中性子は、再び他の「ウラン235」の核分裂を促すスイッチとなます。

つまり一回「ウラン235」に「中性子」を当てると、芋づる式にどんどん反応が起こってしまうのです。

これを核分裂の「連鎖反応」と言います。よくニュースに出てくる「制御棒」は、中性子の数を調整する役割があります。それにより、反応の速さを調整しているわけです。

先ほど紹介したサイトに分かりやすいアニメーションがあるので、リンクを貼っておきます。

核分裂のしくみ ｜ 電気事業連合会

ラボアジエの質量保存の法則

ここで一旦話を18世紀後半に戻します(相対性理論は1905年)。

中学の化学の授業で、「質量保存の法則」というのを習ったのを覚えているでしょうか？

もう少し戻ると、「水素と酸素を化合させる実験」というのを覚えているでしょうか？水上置換法で集めた水素を試験管に入れて、マッチで燃やすと「ポンっ！」と小気味よい音を立てて水ができるというやつです。これを化学式で表すとこのようになります*6。

水素と酸素が化合すると、水ができるという反応です。

 

ここで今話したいのは、図の左辺と右辺では、合計の質量が変わらないという法則があります。

これを「質量保存の法則」と言います。なんかイメージ的にもつきやすいですよね。

 

しかしこれは実は間違っています*7。

間違っているというか、この法則ができた18世紀後半での実験の精度では、このような法則のように見えるということです。

 

時代が変われば実験の技術は高まってきて、より精度の高い実験ができるようになり、既存の法則が適用されなくなるということはよくあります*8。

さきほども言ったように、「質量保存則」でなく「質量＋エネルギー保存則」が成り立つのでしたよね。

 

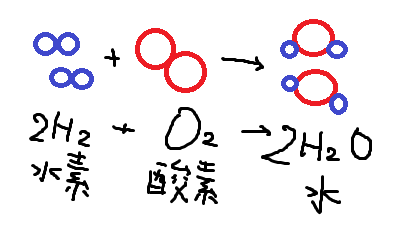
「質量」保存はしない「質量＋エネルギー」保存をする

さきほどのウランの図を貼ります

これは、天秤で表すと、実はこのようになります。

つまり左辺の方が重く、化学反応によって、質量の一部がどこかに飛んでいってしまったのです。

 

ではどこに飛んで行ったのか？それを示す答えがになります。

つまり飛んでいった質量は、「エネルギーと質量の等価性」によって、エネルギーにとって変わられます。そしてエネルギーになり、どこかへ飛んで行ったということです。

つまりこの実験事実が、を表すことになっているのです。

 

原子力発電

原子力発電の話に戻ってこれました。原子力発電は、上で得られた「質量の減少によるエネルギー」を使って、発電しています*9。

莫大なエネルギー効率

原子力発電というと、とにかく「発電効率が良い」ということがあげられますよね。これはなぜなのかと言うと[E=mc^2]を見ることで分かります。

を見ると、エネルギーと質量が比例すると言いましたが、その比例定数である、ここでは何なのかというと光速(光の速さ)でした。

光の速さというのは、1秒で地球7周半移動し、数で表すと真空中では

(m/s)(m/s)

です。これの自乗は、

(m/s)

となります。とんでもなく大きな値ですよね。

 

こんなに大きいものが質量に掛け算されるので、本当にごく少量な質量でも、エネルギーに換算すると莫大な数字になります。実際、さっき出した図

このように人間ほどの体重が、全てエネルギーに変わったら、原発どころではない騒ぎです。「エネルギーありそうやわ～」どころではありません。地球が滅びます。

だいたい1g(つまり一円玉)が全てエネルギーに変わると、約8万世帯の一か月分の消費電力がまかなえるそうです。恐るべしですよね。

 

このようにごく少量の質量から、莫大なエネルギーを得ることができるので、発電のみならず、爆弾としても使われてしまいました。

 

原発などの解説は以上となりますので、以後興味ある人のみお読みください。

 

アインシュタインと原爆

「原爆はアインシュタインがつくった」

これはいろんなところで良く言われていることです。これは半分あっていて、半分間違っているでしょう。

もちろんアインシュタインが手でコネコネして原爆を作ったわけではありませんが、アインシュタインの歴史を簡単に見ていきます。

 

アインシュタインは、ドイツ生まれのユダヤ人です。天才なのも持ってうまれたということでしょうか。

しかしアインシュタインは学校でも行動がとろく、よく仲間から「ノロマ」と言われていたそうです。

 

スイスの大学に進学しますが、成績は良かったわけではなく、物理実験の評価は最低の1、実験中によく爆発も起こしたりしていたそう。

 

大学卒業後は、スイスの国籍を取得し、スイスで公務員として特許に関する仕事をしていたことも有名です。

スイスは時計産業が世界でも群を抜いて発達しており、アインシュタインの元にはたくさんの時計に関する特許の申請があったと言います。アインシュタインはそれによって時間を考えるようになった。なんて本当かどうかも分からない話があったりもします。

 

そして1905年、この年は物理学史の中でも「奇跡の年」と言われています。今年は奇跡の年から110周年ですね。アインシュタインはこの年に「光電効果」「ブラウン運動」「特殊相対論」という超ヘビー級の論文を立て続けに3つ提出。

これは一つ一つがノーベル賞ものであり、物理界に革命を起こす論文でした。だって相対論を超簡単に言うと「まだニュートン力学で消耗してんの？使えないよその理論」だからです。

 

余談ですが、アインシュタインは「相対論」でなく、「光電効果」でノーベル物理学賞を取っています。ノーベル賞は、同じ分野では取れるのは1回だけであり、当時はまだ相対論を証明する実験が無かったからみたいです。*10

 

そしてその2年後の1907年、アインシュタインは相対論の理論からが導かれることを証明します。

 

時代は1914年、第一次大戦です。アインシュタインは平和主義者でも有名であり、徹底的に戦争反対を唱えます。しかし国際事情は無残で、1919アインシュタインの故郷のドイツは敗戦。

 

それのみならず、ヒトラーによるナチスが力をつけてくると、ユダヤ人であるアインシュタイン相対論に対してドイツでの風当たりは強く、アインシュタインはアメリカに逃亡、ドイツに戻ることはありませんでした。

 

第一次大戦、第二次大戦は「科学戦争」で代弁されるように、科学による兵器が大きく発展したときでもありました。こうした負の背景ではありますが、科学は大きく発展し、上に述べた原発に関する開発も次々に行われるようになってきます。

それはアインシュタインの理論を裏付けるものであるとともに、アインシュタインの望みでもある「平和」を打ち壊すものでもありました。

 

1939年、ドイツによる勢力が拡大すると、それを食い止めるために、アインシュタインは、当時のアメリカの大統領であるフランクリン・ルーズベルト宛てに「原子力とその軍事利用の可能性」に触れられた文章を届ます。

これは実際にはアインシュタインは書類にサインをしただけで、文章を作成したわけではないのですが*11、その絶大なる影響力がある人間であるがため、一般的には「アインシュタインのルーズベルト大統領への手紙」とされています。

 

簡単に言えば、アインシュタインがルーズベルトに対して、原爆開発のGoサインを出したということです。

 

そしてその原爆は、無残にも目的であるドイツではなく、日本に向けられてしまいました。

 

1945年5月7日、ドイツは降伏、ここにおいて原爆の役割は終わったはずですが、アメリカは必死の抵抗を続ける日本への使用に方向転換しました。

 

アインシュタインは平和主義であり、日本を心底愛していました。アインシュタインは1922年に日本に来ています。そしてその滞在中に「日本滞在印象記」を書いています。

「日本人のすばらしさは、きちんとした躾や心のやさしさにあるということを、われわれ外国人はじゅうぶん承知していますが、さらに日本社会に対するイメージは、活字になったものであれ、そうでないものであれ、そのようなすばらしさをよりいっそう外国人に強く印象づけているのです」

 

「この国に由来するすべてのものは、愛らしく、朗らかであり、自然を通じてあたえられたものと密接に結びついています」

 

「礼儀正しい人々の絵のように美しい笑顔、お辞儀。座っている姿にただただ驚くばかりですが、しかし真似することはできません」

(「アインシュタイン日本で相対論を語る」より)

日本人から見ても背中がかゆくなる文章ですが、その日本への愛が伝わってくるでしょう。祖国ドイツを食い止めるためにサインしたことも心苦しかったと思いますが、実際に自分が作った理論である原発が日本に落とされたのを聞いて、アインシュタインはどのように感じたのだろうかと思ってしまいます。

 

1955年の「ラッセル・アインシュタイン宣言」というものをご存知でしょうか？これはイギリスの哲学者ラッセルと、アインシュタインが中心となり、冷戦中にアメリカとソ連で競争するように行われていた核兵器の水爆実験を廃止し、科学技術の平和利用を訴えた宣言文です。科学者平和宣言とも言われています。

この宣言は当時、最先端で活躍する科学者の署名がされており、日本人の湯川秀樹のサインもあります。

アインシュタインが亡くなった3か月後に発表されたことから、「アインシュタインの遺言書」とも言われています。世界に発信された科学者のスタンスを表す文章、中には「広島」という言葉も含まれています。当事国である日本人がこれを読まない訳にはいかないと思っています。一度は読んでみてください。

ラッセル・アインシュタイン宣言−日本パグウォッシュ会議

 

先日、ある映画雑誌に掲載されていたキャメロン・ディアスのインタビュー記事を目にした。最後の質問で、何か知りたいことがあるかと尋ねられた彼女は、がいったい何を意味するのか知りたいと答えてきた。ふたりは笑い、そしてディアスの「本気よ」という言葉で記事は終わっていた。そのとき私は思った。という方程式が重要な意味を持っていることは誰でも知っているが、その意味を真に理解している人は少ない。

(「重力とは何か アインシュタインから超弦理論へ、宇宙の謎に迫る (幻冬舎新書)」より)

世界で一番有名な式は、広島・長崎・福島と結びついている。日本人にとって、アインシュタインは他国以上、少なくともキャメロン・ディアスよりは特別な存在であること、そして理科室の壁のポスターにあるが、一旦日本を壊滅させたことは、知っておく価値があるかなと思います。

 

参考図書

メインの参考図書は一番上のです。

アインシュタイン丸かじり―新書で入門 (新潮新書)

重力とは何か アインシュタインから超弦理論へ、宇宙の謎に迫る (幻冬舎新書)

アインシュタイン日本で相対論を語る

入門 現代物理学 - 素粒子から宇宙までの不思議に挑む (中公新書)

*1:言葉に馴染みのない方は、以後「質量」の部分を「重さ」と変換して読んでください

*2:[発展]保存力

*3:運動エネルギー・位置エネルギー・熱エネルギー

*4:僕たちの生活に欠かせない「電磁波」も、マクスウェルによって予言され、後にヘルツが実験で捉えています。

*5:実際は中性子2～3個を放出するそうですが、簡潔さを優先してます

*6:ゆとり世代など、一部の人は習っていない可能性ああります。現在はなんと中2で習いますが

*7:この例のみならず、中学・高校で習う理科の内容というのは、分かりやすさを優先してウソを教えていることはよくあります。

*8:相対性理論が良い例ですね！これによって、ニュートンの法則はとって変わられました。それができたのも、精度の高い「マイケルソン・モーリーの実験」ができたことによります。

*9:発電の仕方は、熱エネルギーによって水を蒸発させて気体にし、体積の差を利用してタービンを回す、というやり方が主流なようです。

*10:キュリー夫人のように、ノーベル化学賞とノーベル物理学賞でとることはできる

*11:文章作成は、アインシュタインの教え子であるレオ・シラード

「慣性系」「静止」ということを深く考えると特殊相対性原理が分かる【止まっているとは何なのか？】

対象：中学生以上(話としては難しいです)

数式：ほぼなし

元記事①：子どもに「相対性理論って何？」と聞かれたときのために概要を分かりやすく簡単に解説してみた - Yukihy Life

元記事②：中学校で習う数学の範囲でアインシュタインの相対性理論を分かりやすく解説する - Yukihy Life

注：この記事は、元ページの補完的役割をしているものですが、独立して読めるようにはしてあります。

高校物理をやった方は、いきなり[４　「止まっている」ことと「等速で動く」こと]に飛んでもOKです。

１　慣性系とは？

特殊相対論が成り立つのは、慣性系のみです。このあたりは元記事①からきた方には説明をしていないので、慣性系の説明をします。

[元記事②から来た人はスキップ開始*1]

慣性系…静止か、等速直線運動をしている世界のこと。

例えば僕たちがスタバの椅子に座って眺めている世界は慣性系の中の静止系という。

また等速で動いている電車の中の世界は慣性系の中の電車の系という。

少しややこしいかもしれませんが、簡単に言えば

①「スタバの椅子から見える世界」(上の文の静止している世界=静止系)

②「等速で動いている電車の中から見える世界*2」(上の文で、等速運動している世界=等速で動く系)

ここでは電車にしましたが、等速運動するものなら新幹線でも何でも良いです。

これら①・②のことを合わせて「慣性系」と言います。

慣性系と対をなすのが「加速度系」です。つまり加速している世界となります。

加速度系…加速している世界のこと

ここでは加速としていますが、減速することも“マイナスに加速する”とすれば加速していることになるので、減速も加速度系に含まれます。

加速度系…加速(減速)している世界のこと

例をあげると

③「加速(減速)している電車の中から見える世界」(加速度系)

とできます。

１のまとめ

日常生活では、世界を①「静止系」②「等速で動く系」③「加速度系」の３つに大別できる。*3

①・②のことを合わせて「慣性系」と言い、③を「加速度系」別名「非慣性系」と言う。*4

[元記事②からきた人スキップ終わり]

２　３つの世界を２つに分ける

スキップした方のために、要点をもう一度書いておくと、僕たちの周りは

①「静止系」ex.スタバの椅子から見える世界

②「等速で動く系」ex.等速で動いている電車の中から見える世界

③「加速度系」ex.加速(減速)している電車の中から見える世界

の３つに分けられます。この記事を見ている今も、このどれかに当てはまると思います。

さて、この３つの世界を２つに分類してくださいと言われたら、皆さんはどのように分類しますか？

つい「①」と「②＆③」で分けませんでした？

おそらくこのように分けた方は「止まっている」か「動いているか」で分けたと思います。

確かにこのような分け方をすると、①「静止系」と②「等速で動く系」＆③「加速度系」に分かれます。

しかし物理では「①＆②」と「③」で分けます。これは①と②を「慣性系」とひとつにくくっていることからも明らかなのです。なぜこのように分けなければいけないのかを次に見ていきます。

２のまとめ

①「静止系」ex.スタバの椅子から見える世界

②「等速で動く系」ex.等速で動いている電車の中から見える世界

③「加速度系」ex.加速(減速)している電車の中から見える世界

の３つの世界を、“直感”で考えるのならば

「①」と「②＆③」

「動いていない」と「動いている」と分けたくなる。

しかし物理ではこれらを

「①＆②」と「③」

「慣性系」と「加速度系」と分ける

３　物理法則は加速しているかどうかで決まる

２のまとめをもう一度書きますと

①「静止系」ex.スタバの椅子から見える世界

②「等速で動く系」ex.等速で動いている電車の中から見える世界

③「加速度系」ex.加速(減速)している電車の中から見える世界

物理では「①＆②」と「③」、「慣性系」と「加速度系」と分ける

なぜこのように分けるのか、経験則から見ていきます。

・例えば止まっている電車の中に座っているとします(①静止系)。止まっているのでまっすぐ座れます。

・電車が動き出し、加速を始めました(③加速度系)。すると体は傾いてしまいます。おなじみの「慣性力」というのがかかっているからです。

・その後電車は同じスピードで進みました(②等速で動く系)。この場合、体はまっすぐに座れると思います。

・最後に電車が減速します(③加速度系)。また体は傾いてしまうでしょう。

この経験則からも、「①＆②」と「③」で分ける理由が分かるのではないでしょうか？③の「加速度系」のときのみ、余分な力*5がかかってきてしまうのです。

「①＆②」は、加速はしていません。(ここで、②は動いていますが、「加速」はしていないことに注意してください。)

極端なことを言えば、等速で動いているものの中ならば、物理法則が変わらずに*6野球だってサッカーだって、地上にいるのと同じようにできてしまうのです。

しかし加速したり減速したりする中では、とてもじゃないですが体がぶれてスポーツなんてできません。

まとめ３

電車の中という経験則から、

「①＆②」では物理法則は変わらない(体は傾かない)

「③」では物理法則が変わってしまう(体が傾いてしまう)

よって、物理では「①＆②」と「③」つまり

「加速していない(慣性系)」と「加速している(加速度系)」というように分類する。

ここまでつまらないことばかり言ってきましたが、４でこの記事で一番言いたかったことをまとめます。

[やや発展]

古典力学の基本法則は、高校の物理で習うです( は質量、は加速度 、は力)。つまり「力」がかかるという物理現象は、物体の「加速度」に影響をします。

「加速度」は「速度」と関係がありますが、「力」と「速度」は直接の関係がないことに着目しなければいけません。

逆に言えば「加速」しているというのは「力」がかかっている場合であり、「静止」していたり「等速」で運動している状態というのは加速していないので、「力」はかかっていないと言えます。

このことから３つの状況を「①＆②」と「③」に分けられると言えます。

[やや発展終わり]

４　「止まっている」ことと「等速で動く」こと

いきなりここにとんできた方のためにまとめます。

①「静止系」ex.スタバの椅子から見える世界

②「等速で動く系」ex.等速で動いている電車の中から見える世界

③「加速度系」ex.加速(減速)している電車の中から見える世界

と３つの世界を考えると、物理では「①＆②」と「③」。

つまり「加速していない」か「加速している」に分かれます。ということです。

[静止とは？]

最後は少し哲学っぽくなります*7。

僕は今、スタバの席からこの記事を書いています。スタバの席なので、系で言えば①の「静止系」です。この記事の中でもずっとスタバの席というのは「静止系」として扱ってきました。

しかし本当にそうでしょうか？

このスタバの席というのを、「僕の目」から見れば、それは間違いなく静止しているでしょう。しかし考えてみると、「地球」というのは自転をしていますよね？そう考えるとスタバの席というのは「静止」とは言えないのではないでしょうか*8。

さらに言えば「地球」というのは静止しているでしょうか？違いますよね。地球と言うのは「太陽系」の中心にある太陽のまわりをすごいスピードでまわっています*9。

「太陽系」は「天の川銀河」のまわりをこれまたすごいスピードでまわっています*10。

それじゃあ銀河の中心は静止しているのかと言うと決してそんなこともなく、宇宙全体は日々動いているのです。

[速さの本質と静止の意味]

ここまで書いてみると、速さというものが何なのか見えてきます。

速さとは“止まっているある点から見るもの(絶対的)”ではなく、“動いている「何」から見た、動いている「何」の速さ(相対的)”と比べなければ意味はなさないのです。

また、このように考えると「静止」という言葉の無意味さにも気づくと思います。

僕は「静止」していると思っていても、天の川銀河の中心から見るとものすごいスピードで動いているわけですし、そもそも静止しているところなんて宇宙上にまだ見つけられていないのです。

[日常的な静止と、物理学上の静止]

日常的に使われている「静止」とは、“地球上の人から見ると”という部分が省略されています。

スタバの例だと、「僕はスタバの席で静止している」という文は誤りで、「僕から見ると僕はスタバの席で静止している」と相対的に使われなければ意味はありません。*11

もっと過激なことを言えば「静止という言葉は地球人の都合で作られた地球人のための造語」とも言えます。全ての生き物が地球で生きているとの仮定の上の言葉であって、地球の外から見れば静止していない訳ですから。

もし僕等よりも文明の発達した宇宙人が来て、僕たちと意思疎通ができるようになったとしても、宇宙人は「静止」なんて言葉持っていないんじゃないかと思います*12。

[まとめ２・まとめ３は嘘]

話を元に戻すと、まとめ２とまとめ３で、

①「静止系」ex.スタバの椅子から見える世界

②「等速で動く系」ex.等速で動いている電車の中から見える世界

③「加速度系」ex.加速(減速)している電車の中から見える世界

というのを「①＆②」と「③」に分かれると言いました。しかしこれは嘘です。①の静止しているというのはありえないからです。

「静止」という言葉を、日常的には使っても良いかもしれませんが、それを物理法則の一つとして特別視することは不可能なのです。僕たちはまだ静止とは何なのか分からないのですから。

それでは「ex.スタバの椅子から見える世界」はどのように解釈されるべきなのでしょう。

これは静止している訳ではなく、太陽から見ても、銀河の中心から見ても、ほぼ等速で運動しているとして良いでしょう*13。つまりこの例は②に加えるべきなのです。

①「静止系」はありえない

②「等速で動く系」ex.等速で動いている電車の中から見える世界＆スタバの椅子から見える世界

③「加速度系」ex.加速(減速)している電車の中から見える世界

つまり僕たちが日常的に感じている「静止」というのは、「等速で動く系」に加えられます。これが今まで「①＆②」とひとくくりにされていた理由でもあるのです。

５　全体のまとめ

結局今回言いたかったことは、「(絶対的な)静止系というのは存在しなく、(日常的に言う)静止していることと等速で動いていることは区別がつかない」というものです。

このことを特殊相対性原理と言います*14。

少し分かりづらい文章になってしまいましたが、ご了承ください。

この「特殊相対性原理」と、もう一つの「光速度不変の原理」という２つの原理から特殊相対論は出来上がります。

特殊相対性原理は、シンプルに説明できたのですが、いずれ書こうと思っている

コラム　特殊相対論はどのようにして生まれたのか(未完成)

で記事にするときに説明しやすいように、少し遠回りして書きました。

*1:とは書いたが、もう一度読むことを推奨します

*2:[発展]本来は直線運動という条件も必要

*3:「系」という言葉が嫌な人は、その部分を「世界」と変えると分かりやすくなるかもしれません。

*4:「非慣性系」というのはややこしいので、この記事では今後使いません。

*5:慣性力

*6:慣性力などの余分な力がかからずに

*7:物理学とはそもそも「時間とはなんだろう」など、哲学から派生したものです。

*8:地球の自転速度は約500m/秒

*9:約30km/秒

*10:約600km/秒

*11:こんなことばっかり言ってると嫌われるので注意してください

*12:こんなことばっかり言ってると嫌われるので注意してください

*13:実際は軌道は若干曲がるので、加速度系に入れるべきですが、大きなスケールで見たとき、ほぼ等速となるので等速とします

*14:[発展]よくある解説本で、「静止系と等速度系の両方は物理法則が変わらないので、両者は同一と見なせる。これを特殊相対性原理と言う」と説明されているのを見るが本質でない。特殊相対性原理の本質は[絶対的な]静止系の否定であり、[絶対的な]静止系を選び出すことは不可能というものである。

相対性理論ってなぜ相対性理論って言うの？【名前の意味で本質が分かる】

対象：中学生以上

数式：なし

元ページ：子どもに「相対性理論って何？」と聞かれたときのために概要を分かりやすく解説してみた - Yukihy Life

 注:このページは、元記事の補足的役割をしています。

０はじめに

相対性理論というと、「時間が遅れる」「空間が曲がる」などという現象を思い浮かべるのではないかと思います。実際こういった現象というのは相対性理論から導かれることなのですが、これらはあくまで相対論の「現象」であって「本質」ではありません。

こういった現象にばかり目を向けていると、その本質が部分が見えなくなってしまい、アインシュタインが最も伝えたかったであろう部分が抜け落ちてしまう可能性があります。

１　相対性理論の「相対性」とは？

展開1

本題です。*1

相対性理論というのはその名の通り、「相対的*2」である理論であります。では何が相対性というのかというと、「長さ」や「時間」のことです。

これらは通常、誰が見ても変わらない。つまり「絶対的*3」なものだと解釈されます。僕が見ても他の人が見ても「50cmものさしは50cm」「１秒は１秒」と思ってしまうからです。

しかし実際は“見る人によって50cmの長さは変わる*4”し、“見る人によって１秒の感じ方は変わる”という「相対的」なものだった。これが相対性理論の本質なのです。

「相対性」と言うからには、何かと何かを比較する必要があります。

つまり相対性理論というものは、必ず“〇〇から見ると、〇〇は、〇〇に見える”と比べる文章になっていなければいけないのです。元のページの結果２・３を書きます。

結果２　光の速度に近い速さで動くものは、縮んで見える(特殊)

結果３　光の速度に近い速さで動くものは、時間が遅く流れる(特殊)

これらの文章は、本来相対性理論の結果を表す部分としてふさわしくありません。上に述べたことを踏まえると、本来

結果２　地球から見ると、光の速度に近い速さで動くものは、縮んで見える(特殊)

結果３　地球から見ると、光の速度に近い速さで動くものは、時間が遅く流れる(特殊)

と比べる文章にしなければいけないのです。*5

ここまでをまとめます。

まとめ①

相対論とは、今まで「絶対的」だと思っていた「長さ」「時間」というもを、見る人によって変わる「相対的」なものととらえる学問である。

展開2

また、「相対的」なものの例として、「速さ」があげられます。

例えば前に歩いている人がいるとします。この人は、止まっている人から見れば、当然前に向かっています。

しかし歩いている人以上のスピードを出している自動車に乗って、そこから見ると歩いている人というのはどんどん後ろに遠ざかって見えます。

つまり「速さ」という概念は、誰が見るかによって変わる「相対的」なものなのです。

しかしここに例外が生まれました。それは「光」です。実験によると光の速さというのは、誰が見ても変わらないもの、つまり「絶対的」なものだったのです*6。

これは光速度不変の原理というものです。

[以下やや発展]

再び例をあげます。止まっている人から光を見たら、当然光の速さで走っているように見えるでしょう。

一方、仮に光の速度の半分で走れる人がいたとして、この人から光を見たらどうでしょう？

光の速さを「相対的」とみるならば、走っている人から見ると光は光の速さの半分の速さで走っているのが見ることができます。

しかし上に述べたように光の速さは「絶対的」なものなので、走っている人から見てもやはり光は光の速さで走っているように見えるのです。

[やや発展終わり]

まとめ②

本来「速さ」とは見る人によって変わる「相対的」なものだが、「光」は例外で「絶対的」なものだった！

２　全体のまとめ

まとめ①とまとめ②をまとめると

①今まで“絶対的”だと思っていた「長さ」と「時間」は、実は“相対的”だった！！

②今まで“相対的”だと思っていた「光の速さ」は、実は“絶対的”だった*7！！

この２つが、相対性理論の本質と言え、相対性理論が相対性理論と呼ばれる所以であります。

ちょうど(距離)=(光の速さ)×(時間)という式に当てはめ(相対的)(絶対的)と色分けすると

相対論ができる前は、

(距離)=(光の速さ)×(時間)

でしたが、相対論ができたあとは、

(距離)=(光の速さ)×(時間)

と、常識を作り替えた理論とも言えます。

余談ですがアインシュタインは、相対性理論を

熱いストーブの上に一分間手をのせてみてください。まるで一時間がぐらいに感じられるでしょう。ところがかわいい女の子と一緒に一時間座っていても、一分間ぐらいにしか感じられない。それが相対性というものです。

と説明しています*8。つまりアインシュタインが最も強調したいのは、「時間が遅れる」とか、「空間が曲がる」とかではなく、現象というのは見る人によって変わる「相対的」なものなんだよ？ということなのです。「時間が遅れる」などというのは枝葉にすぎません*9。

３　時間が遅れている！というのが納得いかない方へ

相対性理論というもので一番ある疑問としては、元記事の

結果３　光の速度に近い速さで動くものは、時間が遅く流れる(特殊)

への疑問です。おそらく時間がの流れが遅れるというのが納得いかないのだと思いますし、僕も思いました。

上で述べたことを使って説明をするのなら、

「時間」というのは“相対的”なものなんだ。だから見る人によって流れる時間というのは変わってしまうんだよ。

というものになります。おそらくこんな説明をしても納得できないのは分かりますが、一つ言えるのは常識の範囲で考えてはいけないということです*10。

物理学は主に数学を使って解いていきますので、「数学がそう表しているからそうなんだ」とも言えます。しかし全ての数学が正しいとは限らないので、様々な検証が行われなければいけません。

相対性理論はこうした検証に耐え、実験結果と整合性がとれる部分が見つかったので、無事理論として成り立ったと言えます。

数式を使った説明は、こちら中学校で習う数学の範囲でアインシュタインの相対性理論を分かりやすく解説する - Yukihy Life

でやっていますので参考にして下さい。

*1:相対論は特殊相対論から始まった理論なので、特殊相対論に重きをおきます

*2:対義語は絶対的

*3:対義語は相対的

*4:錯視ではなく、実際に変わります

*5:元ページは、なるべく文を短くするために入れませんでした。実際、少し難易度をあげた中学校で習う数学の範囲でアインシュタインの相対性理論を分かりやすく解説する - Yukihy Lifeでは入れています。

*6:[発展]ここでは簡潔さを優先してこのように書きましたが、マイケルソン・モーリーの実験から光速度不変が求まるという説は本来論理的に破綻しています。光速度不変とは原理であり、何かから求まるものではないのです。元記事のブコメでも曖昧な方がいたので一応

*7:[発展]何度もしつこいですが、ここでは簡潔さを優先してこのように書いていますが、光速度不変は本来導かれるものでなく要請ということになります。②を要請とすると①が結果として求まるという論理であり、最も重要なのは①であります。

*8:アインシュタインは、物理学による功績のみならず、人に説明する力が非常にあったと言われています。そういった意味でこの一連の記事よりも、アインシュタイン原著の本を読む方が良いのかもしれません。

*9:しかしあまりにも巨大な枝葉です

*10:説明の逃げですね…

子どもに「相対性理論って何？」と聞かれたときのために概要を分かりやすく簡単に解説してみた

この記事の目的はタイトルの通り、子どもに「相対性理論って何？」と聞かれたときに説明できるために、かなりアバウトに相対性理論を解説したものです。

同時に、相対性理論を「まずは概略的にでも理解したい」という方にも有用な内容になっていると思います。

より理解を深めたい方は、こちらの記事にお進み下さい。

• 中学校で習う数学の範囲でアインシュタインの相対性理論を分かりやすく解説する

上のリンクの記事は中学で習う数学のみを使って、相対性理論というものを解説しています。使うのは中学の数学のみですが、扱っている現象は難しいですので、まずはこの記事でイメージを作っていただけれるとスムーズに進めると思います。